Система эвристических методов Г.Д. Балка

Решение. Возможно рассмотреть такие частные случаи нарастающей сложности:

n = 0, m = 1;

n = 0, m = 2;

n = 0, m – любое;

n = 1, m – любое;

n = 2, m – любое ;

n – любое, m – любое (m>n).

Первые три случая тривиальны, поскольку первый игрок может вынуть сразу все шары. В следующих трех случаях первый игрок очевидно должен каждым своим ходом уравнивать количество шаров в соответствии с другим ящиком.

Часто поиск решения предложенной задачи значительно упрощается, если предварительно решить такую вспомогательную задачу, которая имеет сходное условие с данной задачей, но в которой условие или некоторые данные получаются из условия или из данных исходной задачи путем предельного перехода. Например, некоторые из фигур, о которых говорится в исходной задаче, заменяются их предельными положениями. Иначе:

если в исходной задаче идет речь о секущей к окружности, то вместо нее во вспомогательной задаче следует рассмотреть касательную (предельное положение секущей, когда расстояние ее от центра стремится к радиусу);

если в условии задачи говорится о четырехугольнике, то во вспомогательной задаче можно рассматривать треугольник (предельное положение четырехугольника, когда длина одной из его сторон стремится к нулю).

Важно учитывать то, что для одной и той же задачи можно подобрать различные предельные случаи.

Кроме того, рассмотрение предельного случая полезно также при выяснении правдоподобия того или иного готового результата (ответа к задаче, данной формулы), а также для построения опровержения.

Для иллюстрации метода подходит следующая задача.

Задача 14. В четырехугольнике ABCD две стороны AD и BC не параллельны. Что больше: полусумма этих сторон или отрезок MN, соединяющий середины двух других сторон четырехугольника?

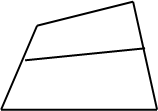Поиск решения. Важно представить, что будет получено в предельном случае, когда В одна из сторон четырехугольника стянется в одну точку. В данном случае стягивать в точку МN можно либо BC (или AD), либо AB (или CD).

Рассмотрим первый случай, тогда пусть BC стянется в точку B. В предельном положении А D точка N совпадет с серединой К отрезка BD, и MN станет средней линией MK

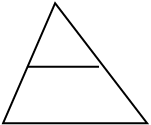Bтреугольника ABD, в предельном случае получаем такую задачу: что больше, половина стороны AD треугольника ABD или отрезок M, соединяющий MK (N)середины двух других сторон?

Ответ прост: MK = AD.

Поставим цель – свести к полученному предельному

ADслучаю решение задачи в общем случае.

Решение. Пусть К – середина диагонали BD четырехугольника ABCD. Из ABD имеем MK = AD и MK || AD. Также из BCD имеем KN = BC и KN || BC.

Статьи о педагогике:

Формирование правовых знаний слушателей в условиях реформирования образования
Во всем мире начиная с 60-х гг. ХХ столетия общественная формация вступила в этап перехода от постиндустриального общества к обществу знаний - обществу, экономика которого основана на знаниях. В настоящее время подчеркивание значения знаний в экономике будущего является одним из наиболее популярных ...

Современное применение технологии коллективного воспитания А.С. Макаренко
Сегодня огромная ценность теории и практики А.С. Макаренко в том, что он сформулировал ряд важных идей в области педагогики: связь воспитания с жизнью, многостороннее воздействие на отношения с помощью деятельности, многообразие внутриколлективных и межколлективных отношений. Несмотря на то, что да ...

Психолого-педагогическая диагностика уровня развития коммуникативных способностей младших школьников
Развитие коммуникативных способностей учащихся предполагает понимание учителем целей обучения речевому общению. Возможности урока, способствующие развитию коммуникативных способностей ученика начальной школы огромны. И в нашей работе, с целью определения уровня сформированности коммуникативных спос ...