Система эвристических методов Г.Д. Балка

Система эвристических приемов Г.Д. Балка имеет в своей основе некоторые методы, рассмотренные выше, такие как введение вспомогательных неизвестных, преобразование задачи в равносильную ей, разбиение задачи на подзадачи. Однако, помимо того, важными для эвристических рассуждений автор считает методы индукции, аналогии, метод рассмотрения предельных случаев, “соображения непрерывности”, метод малых изменений.

Именно эти методы М.Б Балк и Г.Д. Балк практиковали в своей работе в школе еще в 1969 году, считая их базовыми в процессе поиска решения нестандартной задачи. Эти же методы, не включенные в систему эвристических приемов Л.М. Фридмана, подробно будут рассмотрены на примерах решения нестандартных задач в данном пункте.

В математике зачастую имеют место такие случаи, когда аналогичные, сходные условия приводят к сходным результатам. Чтобы таким положением было возможно воспользоваться, необходимо научиться (хотя бы на небольшом числе упражнений) формулировать математические предложения по аналогии. Но также нельзя забывать, что сравнение не является доказательством и предложения, сформулированные по аналогии, могут оказаться ошибочными.

И хотя предложения, сформулированные по аналогии, могут оказаться ошибочными, все же часто оказывается, что такие предложения истинны.

Но не только для формулировки новых правдоподобных математических фактов полезно привлекать аналогию, поскольку еще более ценно научиться сознательно привлекать аналогию при поиске способа решения трудной задачи.

В основном метод аналогии применим при решении геометрических задач (в том числе задач стереометрии по аналогии с планиметрическими).

Рассмотрим пример геометрической задачи, когда найти способ решения позволяет метод аналогии.

Задача 12. Зная стороны треугольника ABC, вычислить радиус r вневписанной окружности, касающейся стороны BC и продолжений сторон AB и AC.

Данная задача не является стандартной, поэтому сразу трудно определить алгоритм ее решения. Но возможно, что из рассмотрения вспомогательной задачи, сформулированной для исходной по аналогии, нетрудно будет найти способ решения исходной. Аналогичная ей может выглядеть следующим образом:

Зная стороны a, b, c треугольника ABC, вычислить радиус r вписанной окружности.

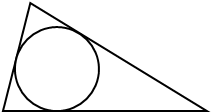Решение. 1. Соединим центр О вписанной окружности с вершинами треугольника ABC.

2. S = S + S + S (1)

3. Обозначим площадь треугольника ABC через S, тогда по формуле Герона

S = .

4. S = cr, S = br, S = ar.

Статьи о педагогике:

Теоретические аспекты обучения старших дошкольников измерительной деятельности и развитие представлений о величине
Вопрос о роли измерений в формировании первых математических представлений ставился еще в работах К.Д. Ушинского [1]. Прогрессивные представители русской методики арифметики также значительное внимание уделяли этой проблеме. Первые советские методисты в области дошкольного воспитания (Е.И. Тихеева, ...

Социально-педагогические предпосылки необходимости воспитания трудолюбия у детей дошкольного возраста
Программные задачи трудового воспитания детей дошкольного возраста можно объединить в несколько групп. Первая группа включает задачи воспитания положительного отношения к труду взрослых, стремления оказывать им посильную помощь, заинтересованность в результатах труда. При этом у детей формируются п ...

Цифровая лаборатория «Архимед» в преподавании химии
Освоение техники работы с использованием цифровой лаборатории «Архимед» позволяет осуществить дифференцированный подход и развить у учащихся интерес к самостоятельной исследовательской деятельности. Эксперименты, проводимые с помощью цифровой лаборатории «Архимед» очень наглядны и эффективны, это д ...