Метод разбиения задачи на подзадачи

Этот метод состоит в том, что сложную нестандартную задачу разбивают на несколько более простых подзадач, по возможности стандартных или ранее решенных, при последовательном решении которых будет решена и исходная сложная задача.

Метод разбиения задачи на подзадачи имеет три разновидности.

Разбиение условий задачи на части.

Разбиение требования задачи на части.

Разбиение области задачи на части.

1)Разбиение условий задачи на части.

Задача 3. Площадь треугольника АВС равна 30 см. На стороне АС взята точка D такая, что AD : DC = 2 : 3. Длина перпендикуляра DE на BC равна 9 см. Найти BC.

Решение. Построим модель данной задачи.

Дано: 1) ∆ABC; S∆ABC = 30 см.

D АС и AD : DC = 2 : 3.

2) DE ^ BC, E 0BC, DE = 9 см.

Найти: ВС.

Внимательно проанализировав условия задачи, нетрудно заметить, что данную нам задачу можно с точностью разделить на две другие, более простые задачи. Переформулировать задачу в две другие возможно так:

Найти площадь треугольника BDC, если сторону AC ∆ABC точка D делит в отношении AD : DC = 2 : 3 и S∆ABC = 30 см².

Найти сторону BC треугольника BDC, зная его площадь и длину высотыDE.

Решаем первую задачу.

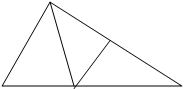
Проведем отрезок BD в ∆ABC. Треугольники

ABD и BDC имеют общую высоту BF, следовательно,В

площади данных треугольников относятся как

длины соответствующих оснований, то есть:Е

S∆ABD : S∆BDС = 2 : 3 ⇒ S∆BDС = (⅗)S∆ABC.

А значит, S∆BDС = (⅗)∙30 = 18 см. А С

Решаем вторую задачу.FD

Для вычисления площади треугольника имеем формулу – половина произведения основания на высоту, поэтому S∆BDС = (½)BC∙DE, то есть, 18 = (½)BC∙9, откуда BC = 4см.

2)Разбиение требования задачи на части.

Задача 4. При каких значениях а корни уравнения

х + х + а = 0 больше а ?

Решение. Требование этой задачи очень сложное. Чтобы сделать суть данной задачи наглядной, разобьем это требование на более простые условия.

Во-первых, чтобы корни данного квадратного уравнения были больше а, они должны вообще существовать на множестве действительных чисел, а для этого дискриминант D должен быть неотрицательным.

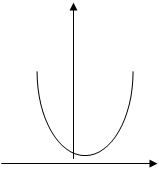
Поскольку коэффициент старшего члена квадратного уравнения равен единице, то ветви данной параболы будут направлены вверх. Тогда при любом значении а значение функции, заданной данным квадратным уравнением, в точке а всегда будет положительно. Это второе условие.

Последнее условие, которое можно извлечь из иx иллюстрации к данной задаче, - абсцисса вершины параболы, всегда строго больше значения а.

Таким образом наша задача разделилась на систему более простых задач:

⇒ ⇒ ;

Статьи о педагогике:

Структура презентаций. Требования к созданию и оформлению презентаций
Структура презентаций Презентация состоит из слайдов. Лучше всего придерживаться одного правила: один слайд – одна мысль. Убедительными бывают презентации, когда на одном слайде дается тезис и несколько его доказательств. Первый лист – это титульный лист, на котором обязательно должны быть представ ...

Воспитание патриотизма – как основа воспитания чувства гражданственности у детей старшего дошкольного возраста
За последнее время вследствие продолжающихся кризисных явлений в социально-экономической, политической, культурной и прочих сферах общественной жизни произошёл резкий спад в деятельности воспитания подрастающего поколения. В настоящее время большое значение приобретает поиск и разработка инновацион ...

Пути реализации метода творческих проектов в общеобразовательной средней школе
Метод проектов – это то дидактическое средство, которое способствует формированию навыков целеполагания, и позволяет учащимся находить оптимальные пути достижения сформулированных целей при соответствующем руководстве со стороны педагога. Он применяется и при коллективной, и при индивидуальной рабо ...