Методы решения задач

= 60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.

Ответ: 20 деталей в день; 60 деталей.

Геометрический метод. Решить задачу геометрическим методом - значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.

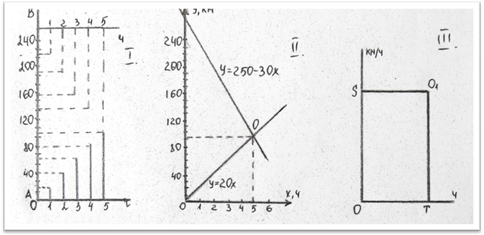
Пример:Из двух городов А и В, расстояние между которыми 250 км, навстречу друг другу выехали два туриста. Скорость движения первого равна 20 км/ч, второго – ЗО км/ч. Через сколько часов туристы встретятся?

Решение.

1-й способ.Математическую модель задачи представим в виде диаграммы. Причем длину одного отрезка по вертикали за 10 км. Длину одного отрезка по горизонтали - за 1 ч. Отложим на вертикальной прямой отрезок АВ

, равный 250 км. Он будет изображать расстояние между городами. Для удобства проведем еще одну ось времени через точку В. затем на вертикальных прямых станем откладывать отрезки пути, пройденные каждым туристом за 1 ч, 2 ч, 3 ч и т. д. Из чертежа видим, что через 5 ч они встретятся.

2-й способ.В прямоугольной системе координат по горизонтали отложим время движения (в часах), по вертикали - расстояние (в километрах).

Примем длину одного отрезка по вертикали за 10 км, а длину одного отрезка по горизонтали - за 1 ч. Построим графики, характеризующие движение каждого туриста. Движение первого туриста определяется функцией v = 20х

, второго -у

— 250-ЗОх

. Абсцисса точки их пересечения (точки О

) указывает, через сколько часов туристы встретятся. Из чертежа видно, что ее значение равно 5. Ордината указывает, на каком расстоянии от пункта А произойдет встреча. Ее значение равно 100.

3-й способ.Пусть время движения туристов до встречи изображается отрезком ОТ

, а скорость сближения - отрезком OS

. Тогда площадь S

прямоугольника OSOT соответствует расстоянию между городами А и В. Учитывая, что туристы сближаются каждый час на 20 + 30 = 50 (км), расстояние между городами равно 250 км, имеем уравнение 250 = 50 * ОТ, решив которое находим ОТ = 5 (ч). Итак, туристы встретятся через 5 ч.

Логический метод. Решить задачу логическим методом - это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения. Примерами таких задач могут служить задачи «на переправы», классическим представителем которых являются задача о волке, козе и капусте, или задачи «на взвешивание». Практический метод. Решить задачу практическим методом - значит найти ответ на требования задачи, выполнив практические действия с предметами или их копиями (моделями, макетами).

Пример.Некто истратил 30 р. Своих денег, после чего удвоил оставшиеся деньги. Затем он истратил 60 р., после чего опять удвоил оставшиеся деньги. Когда он еще истратил 90 р., у него осталось 70р. Сколько денег было вначале?

Решение:

Чтобы определить, сколько денег было первоначально, возьмем оставшееся количество денег и выполним обратные операции в обратном порядке. Берем оставшиеся 70 р., добавляем к ним истраченные 90 р. (160 р.), затем делим эту сумму пополам и узнаем, сколько денег было до того, как второй раз удвоили оставшиеся деньги (80 р.). После этого добавляем 60 р. и находим, сколько денег было до того, как истратили 60 р. (140 р.). Делим эту сумму пополам и узнаем, сколько денег было до того, как первый раз удвоили оставшиеся деньги (70 р.), прибавляем истраченные в первый раз 30 р. и находим первоначальное количество денег (100 р.). Ответ: первоначально было 100 р.

Иногда в ходе решения задачи применяются несколько методов: алгебраический и арифметический; геометрический, алгебраический и арифметический; арифметический и практический и т. д. в этом случае считают, что задача решается комбинированным методом.

Пример.Четыре товарища купили телевизор. Первый внес половину суммы, вносимой остальными, второй - треть того, что внесли все его товарищи, третий - четверть того, что все его товарищи, четвертый - оставшиеся 650 р. Сколько было уплачено за телевизор?

Решение:

Пусть первый товарищ внес х р., второй -у р., третий — z р. тогда, решая задачу чисто алгебраическим методом, по условию задачи получим достаточно громоздкую систему трех уравнений с тремя неизвестными.

Статьи о педагогике:

Лингвострановедение как социокультурный компонент
Основной целью обучения иностранного языка в средней школе является развитие личности школьника в неразрывной связи с преподаванием культуры страны изучаемого языка, способствует желанию «участвовать в межкультурной коммуникации и самостоятельно совершенствоваться в овладеваемой деятельности». Вере ...

Лексико-семантическая работа
Говоря о ходе речевого развития ребенка, А.Н.Леонтьев отмечал, что процесс развития речи не сводится прямому количественному росту, выражающемуся лишь в увеличении словаря ребенка и ассоциативных связей слова, а есть сложный процесс качественных измерений, который охватывает функции, стороны и связ ...

Место силовых упражнений в системе физического воспитания школьников
Ни одно физическое упражнение не мыслимо без проявления силы. Сила мышц в значительной мере определяет быстроту движения и способствует выносливости и ловкости. По данным А.В.Беляева правильный подбор упражнений должен обеспечивать пропорциональное развитие всех участвующих в соревновательном движе ...