Метод моделирования

Так как 2)середины сторон треугольника – основания медиан, то получаем, что каждая медиана этого треугольника имеет на своих концах массы 1 и 2, считая от вершин треугольника.

3) Пользуясь третьим положением, получим, что точка равновесия каждой медианы имеет массу равную трем. Это говорит о том, что точки равновесия медиан совпадают, то есть медианы пересекаются в одной точке. Используя второе положение, получаем, что данной точкой равновесия каждая медиана делится на два отрезка, которые будут находиться в отношении 2 к 1, считая от вершин треугольника.

Векторная модель. Для доказательства данного утверждения необходимо вспомнить формулу деления отрезка в данном отношении для векторов.

Итак, пусть точка M делит отрезок AB так, что AM=λMB (*), тогда для любой точки О выполнимо следующее векторное соотношение: . . , где λ≠ – 1.

Чтобы доказать эту формулу, возьмем векторы и . Подставляя эти соотношения в формулу (*), получаем

, иначе . Группируя векторы, получаем выражение . Отсюда

, где λ≠ – 1.

Решение. Выберем произвольную точку О в качестве общего начала векторов.

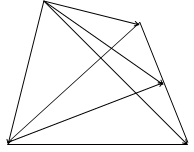На медиане А А возьмем точку G, делящую ее C в отношении 2 : 1, считая от точки А. Тогда на основании формулы деления отрезка в данном отношении будем иметь: и GА₁

.А В

Тогда для произвольной точки О.

В это выражение векторы входят равноправно, поэтому векторы к точкам, делящих медианы в отношении 2 : 1, будут иметь то же выражение. Это означает, что делящие точки совпадают.

Статьи о педагогике:

Работа с воспитателями
Для развития словарного запаса воспитателям можно порекомендовать проводить периодически физкультурные минутки(примеры приведены ниже). 1. Звериная зарядка. Раз - присядка, Два - прыжок. Это заячья зарядка. А лисята как проснуться кулачками потереть глаза Любят долго потянуться потянуться Обязатель ...

Устная речь как форма общения
Современная педагогическая наука рассматривает общение как педагогическую категорию, отражающую субъектно-объектные отношения, которые оказывают самое существенное влияние на весь процесс формирования, воспитания и развития школьника. Общение – это взаимодействие людей, вступающих в него как субъек ...

Диагностика уровня сформированности творческих способностей младших школьников
Для изучения творческих способностей детей младшего школьного возраста на базе МАОУ СОШ №31 города Ишима Тюменской области был проведен эксперимент. В эксперименте приняли участие учащиеся 2 «Е» и 2 «А» классов в количестве 22 человека. 2 «Е» составил экспериментальную группу, 2 «А» контрольную (по ...