Метод моделирования

Этот метод состоит в замене исходной задачи другой задачей, моделью исходной. Примером использования такого метода является широко применяемый метод решения текстовых (сюжетных) задач путем составления уравнения или системы уравнений. Приведем пример использования этого метода.

Задача 8. В квартире десять лампочек. Сколько существует различных способов освещения квартиры? Два способ освещения считаются различными, если они отличаются состоянием хотя бы одной лампочки. Каждая лампочка может гореть и не гореть. Случай, когда все лампочки не горят, - это тоже способ освещения.

Решение. Чтобы легче подсчитать все различные способы освещения квартиры, изобразим каждую лампочку в виде квадрата, а ее состояние будем отмечать знаком “+”, если лампочка горит, и знаком “ – ” в противоположном случае.

Тогда каждому способу освещения квартиры будет соответствовать строка из десяти квадратов со знаком “+” или “ – ”.

Число же таких строк в таблице и есть искомое число различных способов освещения квартиры

Исходя из выше сказанного, получаем следующую задачу.

Имеем прямоугольную таблицу, содержащую 10 столбцов. В каждой клетке стоит “+” или “ – ”. Любые две строки таблицы отличаются знаками в клеточках, стоящих хотя бы в одном и том же столбце. Какое наибольшее число строк имеет эта таблица?

Если решение этой задачи не очевидно, то можно рассматривать каждую строку таблицы, о которой идет речь в предыдущей задаче, как десятичное число, составленное из цифр 1 и 0 ( 1 ~ “+”, 0 ~ “ – ”). Тогда вопрос задачи будет звучать следующим образом: сколько различных десятизначных чисел можно образовать из цифр 0 и 1? (При этом числа, в записи которых слева стоят одни нули, например, 0100001101 или 0000000001 или даже, 0000000000, также рассматриваются).

Решение. На каждом месте в записи десятизначного числа могут стоять лишь цифры 1 и 0. Поэтому имеется лишь две комбинации цифр на каждом месте. Эти комбинации независимы друг от друга, так как проставление цифры на данном месте в записи числа не зависит от того, какие цифры стоят на других местах. Поэтому общее число комбинаций или возможных десятичных различных чисел равно 2 = 1024.

Итак, ответ: общее число способов освещения квартиры равно 1024.

Задача 9. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершин треугольника.

Данная задача легко решается, если построить физическую или векторную ее модели.

Физическая модель. Для построения физической модели нужно вспомнить положения курса физики: 1) центр тяжести двух материальных точек с одинаковой массой лежит в середине отрезка, соединяющего эти точки, с массой, равной сумме масс этих точек;

2) центр тяжести двух материальных точек с различной массой лежит в точке, делящей отрезок в отношении масс (большей массе соответствует меньший отрезок и, наоборот);

3) Центр тяжести системы точек находится путем нахождения центра тяжести пар точек из этой системы, и при этом он не зависит от того , в каком порядке соединяются эти точки попарно.

Решение. Докажем сначала, что медианы треугольника пересекаются в одной точке. Для этого определим центр тяжести системы вершин треугольника. В вершины треугольника – как материальные точки поместим массы по 1 в каждую. Тогда, по 1) положению центр масс каждой пары вершин находится в середине отрезка с концами в этих вершинах.

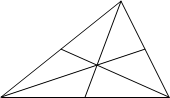Статьи о педагогике:

Требования к составлению тестов
Тестирование, являясь одной из перспективных форм контроля, получает все более широкое применение в учебной практике. Так как основу теста составляют тестовые задания, главным при составлении теста является их правильная разработка. Тестовые задания должны быть прагматически корректными и рассчитан ...

Основные требования к учителю, его функции и мастерство
Если учитель имеет только любовь к делу, он будет хороший учитель. Если учитель имеет только любовь к ученику, как отец, мать, - он будет лучше того учителя, который прочел все книги, но не имеет ни любви к делу, ни к ученикам. Если учитель соединяет в себе любовь к делу и к ученикам - он совершенн ...

Изучение исследования неспособности к обучению при помощи рисуночных тестов
Главной задачей экспериментальной работы было выявление признаков неспособности к обучению у младших школьников. Исследование состояло из двух этапов. На первом этапе - этапе констатирующего среза - была проведена диагностика неспособности к обучению у испытуемых. На втором этапе проводилась оценка ...