Метод преобразования задачи

Если разбить задачу на несколько подзадач невозможно, то следует попытаться ее как-то преобразовать, но, не меняя язык на котором была задана данная задача. Это значит, что если задача была алгебраической, то преобразованная задача тоже должна быть алгебраической, если она была геометрической то преобразованная задача тоже должна быть геометрической и т.д., поскольку если изменится язык, на котором изложена задача, то это уже будет не преобразование, а моделирование, которое будет рассмотрено ниже.

Задача 6. Решить уравнение х =5. (*)

Данное уравнение не степенное, так как показатель х степени – переменная; и не показательное, так как основание степени – переменная. То есть, имеем дело с уравнением неизвестного вида. Сводим данное уравнение к знакомому виду – показательному, используя подстановку:

⇒ (*): х = 5 (**).

Если найдем y из (**), то найдем и х.

,

х = 5.

Исключим из этой системы х, тогда

,

.

Возведем в пятую степень, тогда получим, что . Такое равенство возможно при единственном значении y, а именно y=5, тогда .

Задача 7. Через данную точку А провести прямую таким образом, чтобы ее отрезок с концами на данных прямой и окружности делился точкой А пополам.

Решение. Обозначим искомый отрезок CD, и пусть точка С лежит на окружности, тогда точка D принадлежит прямой m. Поскольку точка А - середина CD, получим, что при центральной симметрии относительно точки

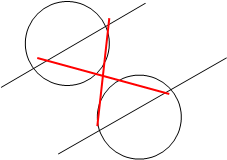Z(m)А точка D перейдет в точку C, и наоборот. aC´ Поэтому данная прямая m и окружность необходимо пересекутся в двух точках или C будут касаться в одной в зависимости от •АD m расположения исходных прямой и окружности. В результате задача сводится к D´m построению образов окружности и прямой при Z(a) центральной симметрии относительно точки А, которые в пересечении с данными прямой m и окружностью a дадут искомые точки C, D, а также C´ и D´. Остается провести требуемую прямую или прямые.

Статьи о педагогике:

Диагностика уровня сформированности положительного отношения к миру труда и профессий у младших школьников
Оценка сформированности качеств личности, определяющих её трудовую воспитанность, имеет свою специфику на каждом возрастном этапе. Экспериментальным путём А.Я. Журкиной и И.И. Зарецкой были выявлены те показатели, которые характеризуют трудовую воспитанность младших школьников. В младшем школьном в ...

Критерии отбора передового педагогического опыта
Для выявления степени эффективности педагогического процесса и его оценки надо иметь критерий, в котором определены: признаки объекта, мера для определения того, в какой степени выражен тот или иной признак у данного объекта. Без этих компонентов нет надёжного критерия и, значит, невозможна объекти ...

Формирование правовых знаний слушателей в условиях реформирования образования
Во всем мире начиная с 60-х гг. ХХ столетия общественная формация вступила в этап перехода от постиндустриального общества к обществу знаний - обществу, экономика которого основана на знаниях. В настоящее время подчеркивание значения знаний в экономике будущего является одним из наиболее популярных ...