Методика изучения перпендикулярности прямых и плоскостей. Методическая схема изучения признака перпендикулярности прямой и плоскости

Содержание: определения: перпендикулярных прямых, перпендикулярных прямой и плоскости, перпендикуляра к плоскости, расстояние от точки до плоскости, наклонной, прямоугольной проекции наклонной, перпендикулярных плоскостей, теоремы о перпендикулярных прямых, признак перпендикулярности прямой и плоскости, теорем о связи между параллельностью и перпендикулярностью прямых и плоскостей в пространстве, теорема о трех перпендикулярах, теорема о перпендикулярных плоскостях.

Т.к. в учебнике Погорелова не вводится понятие о перпендикулярных скрещивающихся прямых то: пряма а, пересекающая плоскость a, называется перпендикулярной к плоскости a, если она перпендикулярна к любой прямой в плоскости a, проходящей через точку пересечения прямой а с плоскостью a.

Определения, приведенные в этой теме, относятся к генетическим (конструктивным), поэтому при их изучении используют методическую схему, определенную в “2” для параллельного проектирования. Согласно определения к плоскости проводим прямую, кот. пересекает ее в некоторой точке А. В этой плоскости найдется прямая, проходящая через точку пересечения.

Если эта прямая перпендикулярна к данной прямой, то ее называют перпендикулярной к плоскости. По рисунку куба попросить учащихся обозначить ребра куба, перпендикулярные к плоскостям AA1BB1, ABCD, D1C1CD, и назвать плоскости, которым перпендикулярны ребра C1D1, A1D1, BC.

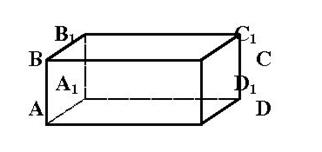
Признак перпендикулярности:

Если прямая, пересекающая плоскость, перпендикулярна к двум прямым в этой плоскости, то она перпендикулярна к плоскости.

Сформулировать эту теорему учащиеся смогут сами, используя приведенную выше задачу (например, ребро А1D1 перпендикулярно к плоскости DD1C1 => А1D1^DD1 и А1D1^D1С1 т.е. двум прямым лежащим в этой плоскости).

Методическая схема изучения признака перпендикулярности прямой и плоскости

подвести учащихся к признаку, сформулировать его;

выполнить рисунок, краткую запись теоремы;

сообщать общую идею доказательства теоремы;

выполнить доп. построения;

сообщать идею доказательства теоремы в более конкретной форме ;

привести план доказательства;

изложить доказательство ;

закрепить доказательство по частям;

воспроизведения доказательства полностью;

Для того чтобы подвести учащихся к теореме можно воспользоваться и др. моделью, состоящей из листа картона и нескольких спиц. С ее помощью показать, что если прямая перпендикулярна только к одной прямой, расположенной в плоскости a, то этого не достаточно, чтобы прямая а была перпендикулярна к плоскости a.

В учебнике дано слово “пересекающиеся” прямые. Здесь приведено традиционное доказательство, основанное на применении признаков равенства треугольников. Одно из первых доп. построений- проведение через точку А произвольной прямой Х, что необходимо для того чтобы доказать справедливость определения прямой, пересекающей плоскость, этой плоскости. Вторая часть доп. построений: AА1=AА2, произвольная прямая СВ, пересекающая прямые b, х, с. А1С, А1Х, А1В, А2С, А2Х, А2В - для образования треугольников, равенство которых будет доказано.

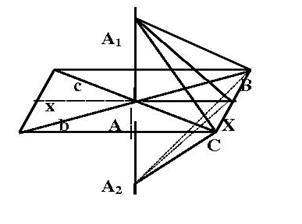
План доказательства:

При наличии подробного плана доказательства краткую запись делать не целесообразно. Оставшаяся часть проводится устно.

Пункт 1 плана можно осуществить, направляя учащихся вопросами типа: Какую фигуру надо рассмотреть? Какое ее свойство нужно установить?

После того как доказано, что для DА1СA2 выполняется равенство А1С=A2С?, Почему А1С=А2С? Почему А1В=А2В? Почему DА2ВС=DА2ВС? и т. п.

Статьи о педагогике:

Соответствие развивающей среды возрасту детей
Все изменения в психологическом содержании деятельности соотносимы с возрастом, имеют ярко выраженную иерархию, что позволяет выстроить психологическое дерево целей развивающей предметной среды детства. Стержень (ствол) этого дерева – возраст ребенка от рождения до 7 лет. Каждый возрастной период ( ...

Определение эффективности театрализованной игры как средства эстетического воспитания дошкольников
Для определения эффективности театрализованной игры как средства эстетического воспитания дошкольников мы провели контрольный эксперимент. Для этого использовали беседу об эстетических представлениях (А.Д. Кошелевой). Результаты беседы представлены в таблице 4. Проанализировав ответы детей можно от ...

Информатизация химического образования
В последнее десятилетие отмечается активное внедрение компьютерных и телекоммуникационных технологий в учебно-воспитательный процесс школы. В системе государственного управления образованием этому вопросу уделяют самое пристальное внимание. Каждый день информационное сообщество российских учителей ...