Методика изучения аксиом стереометрии

Построение системы аксиом стереометрии происходит по двум направлениям: 1) переформулирование аксиом планиметрии для пространства; 2) добавление новых “специфических” аксиом стереометрии.

Первое из них осуществляется через принятие аксиомы: “В каждой плоскости пространства справедливы (выполнимы) все аксиомы планиметрии”. Второе состоит в формулировании нескольких аксиом принадлежности для пространства. В учебнике Погорелова использовано второе направление. Т.к. вводится новый геометрический образ – плоскость, то её основные свойства в пространстве выражают аксиомы:

С1. Какова бы не была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

С3. Если две различные прямые имеют общую точку. То через них можно провести плоскость, и притом только одну.

Таким образом, система аксиом стереометрии состоит из аксиом планиметрии и группы аксиом С.

Методическая схема изучения аксиом стереометрии

Разъяснить абстрактный характер геометрических понятий.

Разъяснить сущность аксиом и их роль в построении геометрии, сформулировать аксиомы.

Проиллюстрировать аксиомы на моделях.

Закрепить аксиомы путём логического анализа их формулировок.

Закрепить аксиомы в процессе их применения к выводу первых следствий геометрии принадлежности в пространстве, к решению задач.

Проиллюстрируем схему на аксиомах группы С.

Понятие плоскость, точка, прямая – абстрактны, т.к. в каждом из случаев отвлекались от свойств ограниченности, линейных размеров, возможной ширины, которыми обладали эти предметы в окружающей действительности.

Перечисленные свойства позволяют строить сечение многогранников, доказывать следствия, вытекающие из аксиом.

В качестве иллюстрации аксиом на модели воспользуемся рисунком куба, по которому учащиеся могут ответить на следующие вопросы: перечислить точки, принадлежащие плоскостям: (ABC),(AA1B1),(D1C1C),(A1B1C1); назвать плоскости, которым принадлежат точки D1,C,B1,A,M,N; назвать линии пересечения плоскостей (AA1D1) и (ABC), (DD1C1) и (BB1C1); имеют ли они общие точки; можно ли провести плоскость через следующие пары прямых: AB и AD, A1B1 и BB1, A1D1 и C1C, BC и AA1.

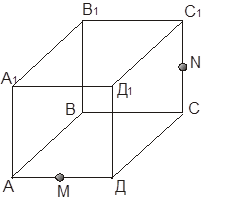
4. Аксиома С1: “Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей”. Её анализ можно направить вопросами: О каких геометрических фигурах говорится в этой аксиоме? - О плоскости и точках. Что именно говорится о плоскости и точках? - На каждой плоскости имеются точки, принадлежащие ей; для каждой плоскости можно указать точки, которые ей не принадлежат. Сколько утверждений сформулировано в аксиоме С1? Сформулируйте их по отдельности. - Сформулированы два утверждения: 1) какова бы ни была плоскость, существуют точки, принадлежащие ей; 2) какова бы ни была плоскость, существуют точки, не принадлежащие ей. Какими другими словами можно заменить слова “какова бы ни была плоскость”?

5. На рисунке изображены две различные плоскости a и b, имеющие общую точку A. Сколько общих точек имеют плоскости a и b?

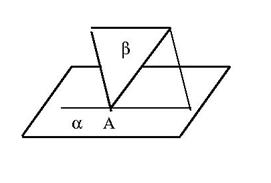
Т.к. плоскости – неограниченны и используя аксиому С2, получаем ответ: бесконечно много точек, расположенных на прямой, являющейся их линией пересечения.

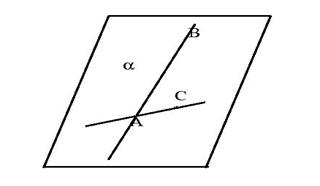
Задача: Можно ли через точку пересечения двух данных прямых провести третью прямую, не лежащую с ними в одной плоскости? Объясните ответ.

По аксиоме С3 пересекающиеся данные прямые задают положение одной из плоскостей в пространстве. В пространстве найдётся прямая, не принадлежащая данной плоскости (применяем аксиому С1, по которой выбрав любую точку, не принадлежащую построенной плоскости, и точку пересечения данных прямых, строим искомую прямую). Такую прямую можно построить.

Роль аксиом в построении геометрии хорошо видна при доказательстве первых следствий, которые в действующем учебнике представлены в виде теорем.

Т.15.1. Через прямую и не лежащую на ней точку можно построить плоскость, и притом только одну.

Для лучшего выделения всех предложений, используемых при доказательстве следствия, целесообразно доказательство оформить в виде таблицы с двумя колонками “утверждения” и “на основании”.

Статьи о педагогике:

Развитие здорового школьника и осанки
Осанка в основном формируется в 6–7 лет, это связано с основными задачами предмета «Физическая культура» и проводится с учетом возрастных особенностей развития учащихся. Дети 6–9 лет находятся в периоде интенсивного биологического развития и активного освоения различных форм школьного труда. В связ ...

Эмоции и чувства
Эмоции – особый класс субъективных психологических состояний, отражающих в форме непосредственных переживаний процесс и результаты практической деятельности человека. Эмоции, утверждал Ч. Дарвин, возникли в процессе эволюции как средство, при помощи которого живые существа устанавливают значимость ...

Понятие, виды, и мотивы противоправного поведения школьников
Как сказано в юридической энциклопедии, право — это совокупность установленных или сан­кционированных государством общеобязательных пра­вил поведения (норм), соблюдение которых обеспечива­ется мерами государственного воздействия. А в учебнике Конституционного права говорится, что современном общест ...