Методика изучения параллельности прямых и плоскостей

Содержание: определения параллельных и скрещивающихся прямых в пространстве, теорема о существовании и единственности прямой, проходящей через данную точку параллельно данной прямой, транзитивность параллельности прямых, параллельность прямой и плоскости (определение и признак), параллельность плоскостей (определение и признак), изображение пространственных фигур на плоскости.

Наряду с обычными целями обучения геометрии здесь большую роль играет цель формирования у учащихся пространственного представления и воображения.

Методика изучения определения параллельных и скрещивающихся прямых построена с помощью логической операции отрицания: “Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются”. “Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися”. Точный смысл понятий: “прямые не пересекаются”, “прямые не лежат в одной плоскости” может быть получен с помощью операции отрицания понятий “прямые пересекаются”, “прямые лежат в одной плоскости”.

Методическая схема изучения параллельных и скрещивающихся прямых в пространстве

Сообщить определения;

проиллюстрировать эти понятия на модели куба, классной комнате, рисунке;

провести логический анализ формулировки определения;

выполнить задания на нахождение параллельных и скрещивающихся прямых на модели (рисунке) куба;

сопроводить показ параллельных и скрещивающихся прямых соответствующими обоснованиями.

Для облегчения логического анализа определений и построения отрицания полезно на доске выполнить следующие записи:

прямые a и b пересекаются: имеют общую точку, и притом только одну;

прямые a и b не пересекаются: не имеют общих точек или общих точек более одной.

Понятие параллельного проектирования вводится с помощью генетического определения. В соответствии с общей особенностью генетических определений используется методическая схема изучения параллельного проектирования:

одновременно проговорить определения и произвести построения (выполняется учителем);

одновременно проговорить определения и показать соответствующие построения на готовом рисунке (выполняется учеником); стереть имеющийся на доске рисунок;

одновременно проговорить определение и выполнить новый рисунок (выполняется учеником).

Методику изучения теорем и их доказательств рассмотрим на примере признака параллельности прямой и плоскости: “Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости”.

Методическая схема:

подвести учащихся к теореме, сформулировать ее;

выполнить рисунок, краткую запись теоремы;

сообщать общую идею теоремы;

привести план доказательства;

предоставить учащимся возможность самостоятельно осуществить док-во;

осуществить доказательство (ученик);

закрепить доказательство путем его воспроизведения;

применить теорему к решению задач.

Подведение учащихся к теореме: на стол положим спицу а1, вторую спицу положим так, чтобы она была параллельна спице а1.

Вопрос: что можно сказать о взаимном расположении спицы а и поверхности стола?

После опыта задается вопрос: Какую теорему можно сформулировать?

Идея доказательства: (после выполнения рисунка и краткой записи теоремы).

Выполним доп. построение: через параллельные прямые а и а1 проведем плоскость a1.

Док-во от противного:

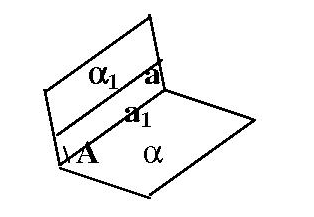
Учтем, что все общие точки плоскостей a и a1 должны принадлежать прямой а1.

План доказательства:

проводим плоскость a1;

делаем допущение, что а не параллельна a;

рассмотрим точку А, точку пересечения прямой а и плоскости a;

приходим к выводу, что прямые а и а1 пересекаются;

противоречие;

а//a.

После проведения доказательства решим следующую задачу:

Статьи о педагогике:

Социально-педагогические предпосылки необходимости воспитания трудолюбия у детей дошкольного возраста
Программные задачи трудового воспитания детей дошкольного возраста можно объединить в несколько групп. Первая группа включает задачи воспитания положительного отношения к труду взрослых, стремления оказывать им посильную помощь, заинтересованность в результатах труда. При этом у детей формируются п ...

Основные направления развития педагогической науки и ее взаимосвязи с практикой
Перестройка и обновление нашего общества затрагивают все об­ласти его материальной и духовной жизни. Не является исключени­ем и педагогическая наука. Ее общественное значение определяется тем реальным вкладом, который она может внести в решение про­блем реформы высшей и средней школы, в научно-мето ...

Место психологии в системе наук
Психология имеет многогранные связи, как с естественными, так и с социальными науками. Теоретико-методологической основой психологии является философия. С естественными науками психология связана общетеоретическими положениями, которые используются для обоснования закономерностей развития психики, ...